Basic Statistics


An overview of basic statistics in R

By: Valentina Urrutia Guada for UQRUG

Basic Statistics

This is simply a presentational form of the code shown during the August UQRUG.

Click for the external link to these slides

Load the libraries and data

#Packages and libraries
library(tidyverse)
library(lattice)

#Loading data
data1<-mtcars
data2<-read.csv("datasets/ttest.csv")
data3<-read.csv("datasets/ANOVA.csv")
data4<-read.csv("datasets/correl.csv")

#Creating objects
Y<-mtcars$mpg
X<-mtcars$wt

Explore the data structure

#Basic exploration of data
View(data1)
str(data1)
'data.frame':   32 obs. of  11 variables:
 $ mpg : num  21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
 $ cyl : num  6 6 4 6 8 6 8 4 4 6 ...
 $ disp: num  160 160 108 258 360 ...
 $ hp  : num  110 110 93 110 175 105 245 62 95 123 ...
 $ drat: num  3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
 $ wt  : num  2.62 2.88 2.32 3.21 3.44 ...
 $ qsec: num  16.5 17 18.6 19.4 17 ...
 $ vs  : num  0 0 1 1 0 1 0 1 1 1 ...
 $ am  : num  1 1 1 0 0 0 0 0 0 0 ...
 $ gear: num  4 4 4 3 3 3 3 4 4 4 ...
 $ carb: num  4 4 1 1 2 1 4 2 2 4 ...

Descriptive statistics

The summary() function provides quick and easy descriptive statistics, and is useful initial step:

summary(data1)
      mpg             cyl             disp             hp       
 Min.   :10.40   Min.   :4.000   Min.   : 71.1   Min.   : 52.0  
 1st Qu.:15.43   1st Qu.:4.000   1st Qu.:120.8   1st Qu.: 96.5  
 Median :19.20   Median :6.000   Median :196.3   Median :123.0  
 Mean   :20.09   Mean   :6.188   Mean   :230.7   Mean   :146.7  
 3rd Qu.:22.80   3rd Qu.:8.000   3rd Qu.:326.0   3rd Qu.:180.0  
 Max.   :33.90   Max.   :8.000   Max.   :472.0   Max.   :335.0  
      drat             wt             qsec             vs        
 Min.   :2.760   Min.   :1.513   Min.   :14.50   Min.   :0.0000  
 1st Qu.:3.080   1st Qu.:2.581   1st Qu.:16.89   1st Qu.:0.0000  
 Median :3.695   Median :3.325   Median :17.71   Median :0.0000  
 Mean   :3.597   Mean   :3.217   Mean   :17.85   Mean   :0.4375  
 3rd Qu.:3.920   3rd Qu.:3.610   3rd Qu.:18.90   3rd Qu.:1.0000  
 Max.   :4.930   Max.   :5.424   Max.   :22.90   Max.   :1.0000  
       am              gear            carb      
 Min.   :0.0000   Min.   :3.000   Min.   :1.000  
 1st Qu.:0.0000   1st Qu.:3.000   1st Qu.:2.000  
 Median :0.0000   Median :4.000   Median :2.000  
 Mean   :0.4062   Mean   :3.688   Mean   :2.812  
 3rd Qu.:1.0000   3rd Qu.:4.000   3rd Qu.:4.000  
 Max.   :1.0000   Max.   :5.000   Max.   :8.000

Visualise the data

With histogram() we can quickly view the descriptive stats plots per variable

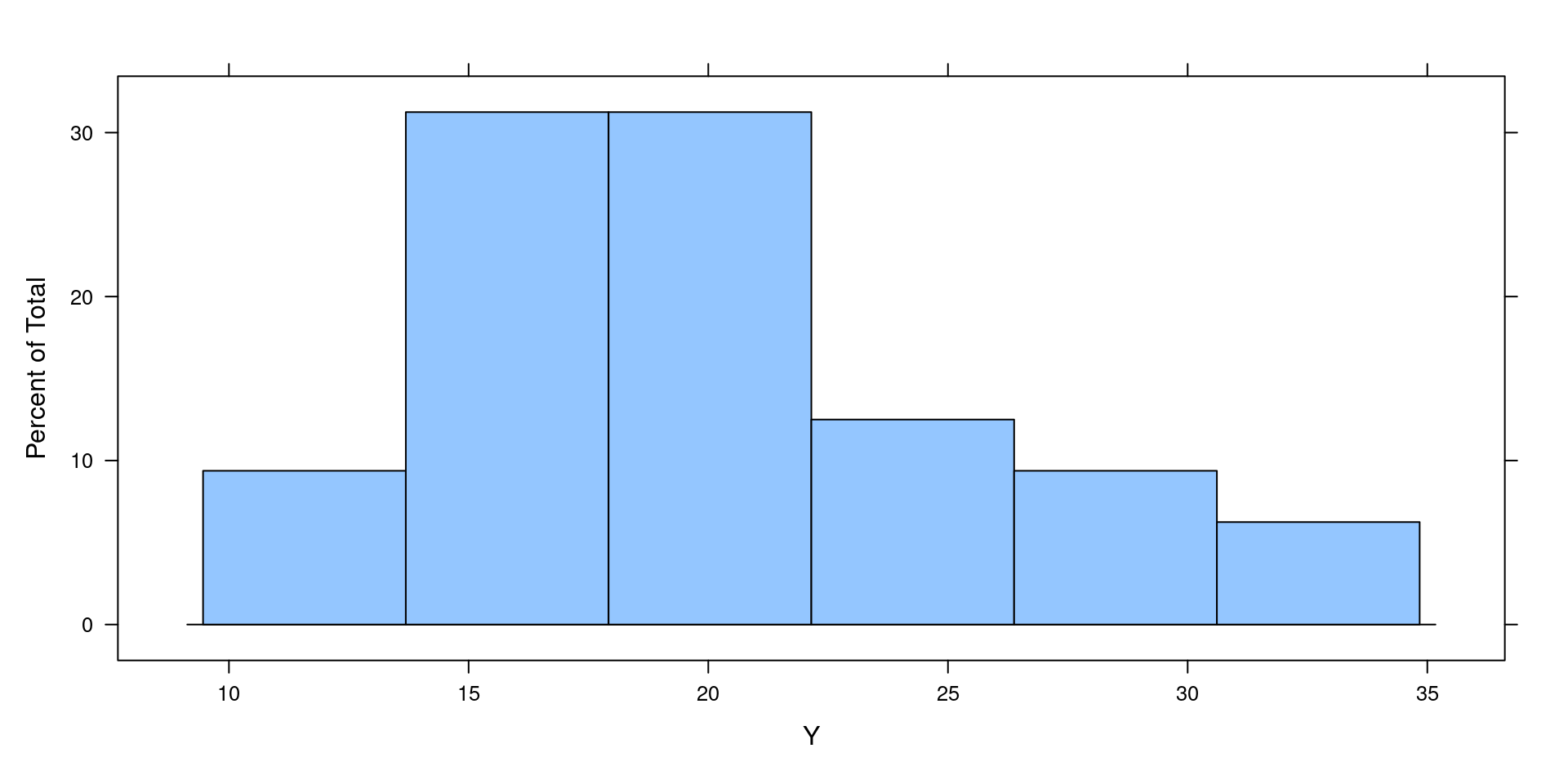
histogram(Y) # the same as histogram(data$Y) or histogram(~Y,data)

Visualise the data

Box and whisker plots are another useful way to visualise our data spread quickly and easily with bwplot()

bwplot(Y)

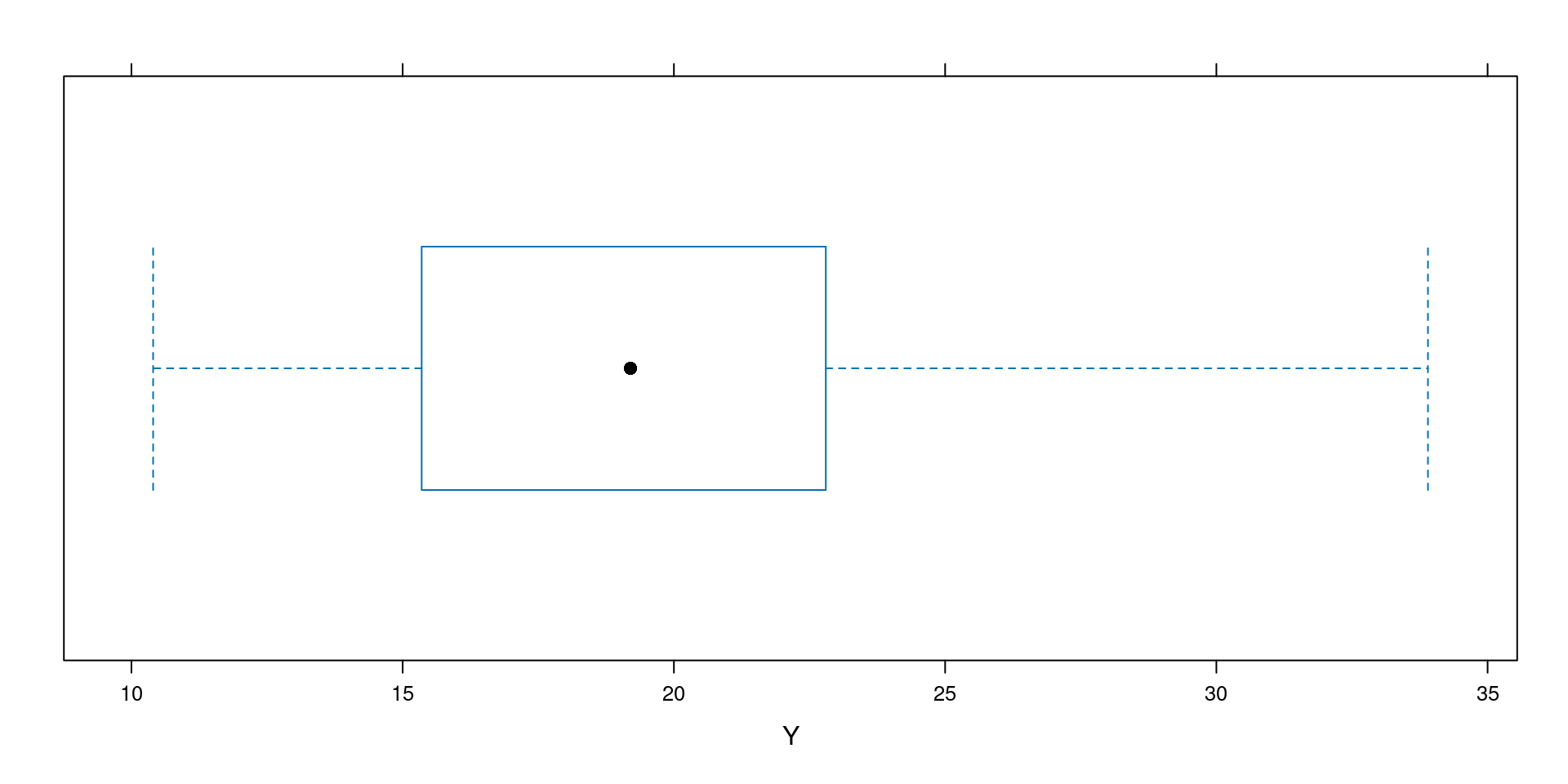
Inferential statistics

The classic two sample t-test can easily be run with the t.test() function

#two sample t-test
t.test(time~daytime,data2)

    Welch Two Sample t-test

data:  time by daytime
t = -6.8311, df = 77.776, p-value = 1.667e-09
alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0
95 percent confidence interval:
 -48.78467 -26.76533
sample estimates:
mean in group 1 mean in group 2 
        967.900        1005.675

ANOVA visualisation

Before we run the ANOVA test, it can be a good idea to visualise our data with a boxplot, which ggplot2 also has

#ANOVA aov(Y ~ X, data)
ggplot(data3)+
  aes(mode, students, group = mode)+
  geom_boxplot()

ANOVA

An ANOVA is a good test to determine if the means of multiple independent variables are equal

summary(aov(students~mode,data=data3))
            Df Sum Sq  Mean Sq F value Pr(>F)  
mode         1 0.0191 0.019093   2.953 0.0889 .
Residuals   97 0.6272 0.006466                 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation

Before running a corrlelation test, it is good to visualise the relationship of the data with a simple scatterplot such as the lattice xyplot()

#Relationship
#Scatterplot
xyplot(FXRUSD~FXREUR,data4)

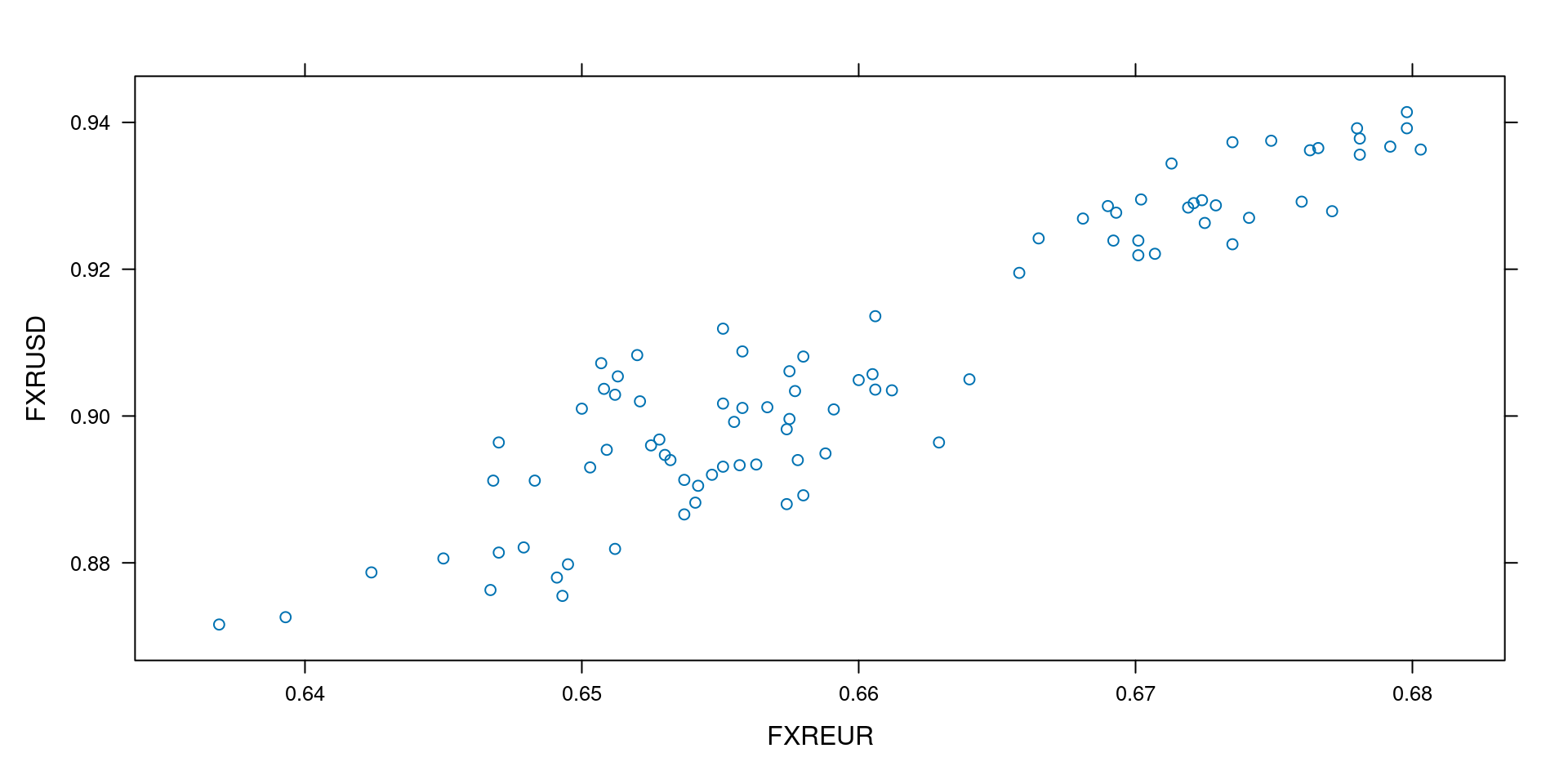
Correlation

We can now test for correlation using a Pearson or Spearman test

#correlation (Pearson)
cor(data4$FXRUSD,data4$FXREUR,method="pearson")
[1] 0.933557
#correlation (Spearman)
cor(data4$FXRUSD,data4$FXREUR,method="spearman")
[1] 0.872435

Linear Regression

#linear regression
lm(FXRUSD~FXREUR,data4)

Call:
lm(formula = FXRUSD ~ FXREUR, data = data4)

Coefficients:
(Intercept)       FXREUR  
     -0.190        1.662